La stéréométrie est une partie importante du cours de géométrie générale, qui examine les caractéristiques des figures spatiales. L'une de ces figures est un prisme quadrangulaire. Dans cet article, nous allons révéler plus en détail la question de savoir comment calculer le volume d'un prisme quadrangulaire.
Qu'est-ce qu'un prisme quadrangulaire ?
Évidemment, avant de donner la formule du volume d'un prisme quadrangulaire, il faut donner une définition claire de cette figure géométrique. Un tel prisme est compris comme un polyèdre tridimensionnel, qui est délimité par deux quadrangles identiques arbitraires situés dans des plans parallèles et quatre parallélogrammes.
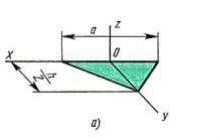
Les quadrangles parallèles marqués sont appelés les bases de la figure, et les quatre parallélogrammes sont les côtés. Il convient de préciser ici que les parallélogrammes sont aussi des quadrangles, mais les bases ne sont pas toujours des parallélogrammes. Un exemple d'un quadrilatère irrégulier, qui pourrait bien être la base d'un prisme, est montré dans la figure ci-dessous.

Tout prisme quadrangulaire a 6 côtés, 8 sommets et 12 arêtes. Il existe différents types de prismes quadrangulaires. Par exemple, une figure peut être oblique ou droite, irrégulière et correcte. Plus loin dans l'article, nous montrerons comment calculer le volume d'un prisme quadrangulaire, en tenant compte de son type.

Prisme oblique avec mauvaise base
C'est le type de prisme quadrangulaire le plus asymétrique, donc le calcul de son volume sera relativement difficile. L'expression suivante permet de déterminer le volume d'une figure :
Le symbole So désigne ici la zone de base. Si cette base est un losange, un parallélogramme ou un rectangle, alors il n'est pas difficile de calculer la valeur de So. Ainsi, pour un losange et un parallélogramme, la formule suivante est valable :
où a est le côté de la base, ha est la longueur de la hauteur tombant de ce côté depuis le haut de la base.

Si la base est un polygone irrégulier (voir ci-dessus), alors son aire doit être divisée en formes plus simples (par exemple, des triangles), calculer leurs aires et trouver leur somme.
Dans la formule du volume, h représente la hauteur du prisme. C'est la longueur de la ligne perpendiculaire entre deux bases. Comme le prisme est incliné, la hauteur h doit être calculée en utilisant la longueur du bord latéral b et les angles dièdres entre les bords latéraux et la base.
Chiffre correct et son volume
Si la base d'un prisme quadrangulaire est un carré et que la figure elle-même est droite, alors elle est dite régulière. Il convient de préciser qu'un prisme droit est appelé lorsque tous ses côtés latéraux sont des rectangles et que chacun d'eux est perpendiculaire aux bases. Le chiffre correct est indiqué ci-dessous.

Le volume d'un prisme quadrangulaire régulier peut être calculé en utilisant la même formule que le volume d'une figure irrégulière. Puisque la base est un carré, son aire se calcule simplement :
La hauteur du prisme h est égale à la longueur de la nervure latérale b (côté du rectangle). Ensuite, le volume d'un prisme quadrangulaire régulier peut être calculé en utilisant la formule suivante :
Un prisme régulier à base carrée est appelé parallélépipède rectangle. Ce parallélépipède, en cas d'égalité des côtés a et b, devient un cube. Le volume de ce dernier est calculé comme suit :
Les formules écrites pour le volume V indiquent que plus la symétrie de la figure est élevée, moins il faut de paramètres linéaires pour calculer cette valeur. Ainsi, dans le cas d'un prisme correct, le nombre de paramètres requis est de deux, et dans le cas d'un cube, un.
Le problème avec le bon chiffre
Ayant considéré la question de trouver le volume d'un prisme quadrangulaire du point de vue théorique, nous appliquerons les connaissances acquises dans la pratique.
On sait qu'un parallélépipède régulier a une longueur de diagonale de base de 12 cm. La longueur de la diagonale de son côté latéral est de 20 cm. Il est nécessaire de calculer le volume du parallélépipède.
Notons la diagonale de la base par le symbole da, et la diagonale de la face latérale par le symbole db. Pour la diagonale da, les expressions suivantes sont valides :
Quant à la valeur db, c'est la diagonale d'un rectangle de côtés a et b. Pour cela, vous pouvez écrire les égalités suivantes :
db2 = a2 + b2 =>
b = (db2 - a2)
En substituant l'expression trouvée pour a dans la dernière égalité, on obtient :
b = (db2 - da2 / 2)
Vous pouvez maintenant substituer les formules résultantes dans l'expression du volume d'une figure régulière :
V = a2 * b = da2 / 2 * √ (db2 - da2 / 2)
En remplaçant da et db par les nombres de l'énoncé du problème, nous arrivons à la réponse : V 1304 cm3.
Un prisme est une figure volumétrique géométrique assez simple. Néanmoins, certains écoliers ont du mal à définir ses propriétés de base, la raison pour laquelle, en règle générale, est associée à une terminologie mal utilisée. Dans cet article, nous examinerons ce que sont les prismes, comment ils s'appellent et décrirons également en détail le prisme quadrangulaire correct.
Prisme en géométrie
L'étude des figures volumétriques est la tâche de la stéréométrie - une partie importante de la géométrie spatiale. En stéréométrie, un prisme est compris comme une figure formée par la translation parallèle d'un polygone plat arbitraire à une certaine distance dans l'espace. La translation parallèle implique un tel mouvement dans lequel la rotation autour d'un axe perpendiculaire au plan du polygone est totalement exclue.
Vous serez intéressé par :
A la suite du procédé décrit d'obtention d'un prisme, une figure est formée, limitée par deux polygones ayant les mêmes dimensions, situés dans des plans parallèles, et un certain nombre de parallélogrammes. Leur nombre coïncide avec le nombre de côtés (sommets) du polygone. Les polygones identiques sont appelés bases de prismes et leur surface est l'aire des bases. Des parallélogrammes reliant deux bases forment une surface latérale.
Éléments prismatiques et théorème d'Euler
Étant donné que la figure volumétrique considérée est un polyèdre, c'est-à-dire qu'elle est formée d'un ensemble de plans sécants, elle est caractérisée par un certain nombre de sommets, d'arêtes et de faces. Ce sont tous des éléments d'un prisme.
Au milieu du XVIIIe siècle, le mathématicien suisse Leonard Euler a établi une relation entre le nombre d'éléments de base d'un polyèdre. Cette relation s'écrit avec la formule simple suivante :
Nombre d'arêtes = nombre de sommets + nombre de faces - 2
Pour tout prisme, cette égalité est vraie. Donnons un exemple de son utilisation. Supposons que vous ayez un prisme quadrangulaire régulier. Il est montré dans la figure ci-dessous.

On peut voir que le nombre de sommets pour elle est de 8 (4 pour chaque base quadrangulaire). Le nombre de côtés, ou faces, est de 6 (2 bases et 4 rectangles latéraux). Alors le nombre d'arêtes pour cela sera :
Nombre de côtes = 8 + 6 - 2 = 12
Classification complète des prismes
Il est important de comprendre cette classification afin de ne pas vous perdre dans la terminologie plus tard et d'utiliser les formules correctes pour calculer, par exemple, la surface ou le volume des figures.
Pour tout prisme de forme arbitraire, on peut distinguer 4 caractéristiques qui le caractériseront. Listons-les :
- Par le nombre de coins du polygone à la base : triangulaire, pentagonal, octogonal, etc.
- Comme un polygone. Cela peut être vrai ou faux. Par exemple, un triangle rectangle est irrégulier et un triangle équilatéral est régulier.
- Par le type de convexité d'un polygone. Il peut être concave ou convexe. Les prismes convexes sont les plus courants.
- Aux angles entre les bases et les parallélogrammes latéraux. Si tous ces angles sont à 90o, alors ils parlent d'un prisme droit, sinon tous ne sont pas droits, alors une telle figure est appelée oblique.
De tous ces points, je voudrais m'attarder sur ce dernier plus en détail. Un prisme droit est aussi appelé rectangulaire. Cela est dû au fait que pour elle les parallélogrammes sont des rectangles dans le cas général (dans certains cas ils peuvent être des carrés).

Par exemple, la figure ci-dessus montre une forme rectangulaire concave pentagonale ou droite.
La base de ce prisme est un quadrilatère régulier, c'est-à-dire un carré. La figure ci-dessus a déjà montré à quoi ressemble ce prisme. En plus des deux carrés qui le délimitent en haut et en bas, il comprend également 4 rectangles.

Désignons le côté de la base d'un prisme quadrangulaire régulier par la lettre a, et désignons la longueur de son bord latéral par la lettre c. Cette longueur est aussi la hauteur de la figure. Alors l'aire de toute la surface de ce prisme sera exprimée par la formule :
S = 2 * a2 + 4 * a * c = 2 * a * (a + 2 * c)
Ici, le premier terme traduit la contribution des bases à la surface totale, le second terme est la surface latérale.
Compte tenu des désignations introduites pour les longueurs des côtés, nous écrivons la formule pour le volume de la figure en question:
C'est-à-dire que le volume est calculé comme le produit de la surface de base carrée par la longueur de la nervure latérale.
Cube de figurines
Tout le monde connaît cette figure tridimensionnelle idéale, mais peu de gens pensaient qu'il s'agissait d'un prisme quadrangulaire régulier, dont le côté est égal à la longueur du côté de la base carrée, c'est-à-dire c = a.
Pour un cube, les formules de la surface totale et du volume prendront la forme :
Puisqu'un cube est un prisme composé de 6 carrés identiques, toute paire parallèle d'entre eux peut être considérée comme une base.

Un cube est une figure hautement symétrique qui est naturellement réalisée sous la forme de réseaux cristallins de nombreux matériaux métalliques et cristaux ioniques. Par exemple, les réseaux d'or, d'argent, de cuivre et de sel de table sont cubiques.
Dans le programme scolaire du cours de stéréométrie, l'étude des figures volumétriques commence généralement par un corps géométrique simple - un polyèdre d'un prisme. Le rôle de ses bases est joué par 2 polygones égaux situés dans des plans parallèles. Un cas particulier est un prisme quadrangulaire régulier. Ses bases sont 2 quadrangles réguliers identiques, auxquels les côtés latéraux sont perpendiculaires, en forme de parallélogrammes (ou de rectangles si le prisme n'est pas incliné).
A quoi ressemble un prisme
Un prisme quadrangulaire régulier s'appelle un hexagone, à la base duquel se trouvent 2 carrés, et les faces latérales sont représentées par des rectangles. Un autre nom pour cette figure géométrique est un parallélépipède droit.
Un dessin montrant un prisme quadrilatéral est montré ci-dessous.
La photo montre aussi les éléments les plus importants qui composent un corps géométrique... Il est d'usage de les désigner :
Parfois, dans les problèmes de géométrie, on peut trouver le concept de section. La définition ressemblera à ceci : une section est tous les points d'un corps volumétrique qui appartiennent à un plan de coupe. La section est perpendiculaire (elle coupe les bords de la figure à un angle de 90 degrés). Pour un prisme rectangulaire, une section diagonale est également considérée (le nombre maximum de sections pouvant être construites est de 2) passant par 2 arêtes et diagonales de la base.

Si la section est dessinée de telle sorte que le plan de coupe ne soit parallèle ni aux bases ni aux faces latérales, le résultat est un prisme tronqué.
Diverses relations et formules sont utilisées pour trouver les éléments prismatiques réduits. Certains d'entre eux sont connus du cours de planimétrie (par exemple, pour trouver l'aire de la base d'un prisme, il suffit de rappeler la formule de l'aire d'un carré).
Superficie et volume
Pour déterminer le volume d'un prisme à l'aide de la formule, vous devez connaître l'aire de sa base et sa hauteur :
V = S principal h
Puisque la base d'un prisme tétraédrique régulier est un carré de côté une, vous pouvez écrire la formule plus en détail :
V = a²h
Si nous parlons d'un cube - un prisme régulier de longueur, largeur et hauteur égales, le volume est calculé comme suit :
Pour comprendre comment trouver l'aire de la surface latérale d'un prisme, il faut imaginer son déroulement.

Le dessin montre que la surface latérale est composée de 4 rectangles égaux. Son aire est calculée comme le produit du périmètre de la base et de la hauteur de la figure :
Côté = P principal h
Compte tenu du fait que le périmètre du carré est P = 4a, la formule prend la forme :
Côté = 4a h
Pour un cube :
Côté = 4a²
Pour calculer la surface totale du prisme, ajoutez 2 surfaces de base à la surface latérale :
S plein = côté S + 2S principal
Par rapport à un prisme quadrangulaire régulier, la formule est :
S total = 4a · h + 2a²
Pour la surface d'un cube :
S total = 6a²
Connaissant le volume ou la surface, vous pouvez calculer les éléments individuels du corps géométrique.
Trouver des éléments de prisme
Il y a souvent des problèmes dans lesquels un volume est donné ou la valeur de la surface latérale est connue, où il est nécessaire de déterminer la longueur du côté de la base ou la hauteur. Dans de tels cas, les formules peuvent être dérivées :
- longueur côté base: a = côté S / 4h = (V / h) ;
- longueur de hauteur ou nervure latérale: h = Côté / 4a = V / a² ;
- surface de base : Sosn = V/h;
- surface latérale du visage : côté S. gr = côté S / 4.
 Pour déterminer l'aire d'une section diagonale, vous devez connaître la longueur de la diagonale et la hauteur de la figure. Pour un carré d = a√2. Par conséquent:
Pour déterminer l'aire d'une section diagonale, vous devez connaître la longueur de la diagonale et la hauteur de la figure. Pour un carré d = a√2. Par conséquent:
Sdiag = ah√2
Pour calculer la diagonale du prisme, utilisez la formule :
dprize = √ (2a² + h²)
Pour comprendre comment appliquer les ratios ci-dessus, vous pouvez vous entraîner et résoudre quelques tâches simples.
Exemples de tâches avec des solutions
Voici quelques-unes des tâches trouvées dans les examens finaux d'État en mathématiques.

Exercice 1.
Le sable est versé dans une boîte en forme de prisme quadrangulaire régulier. La hauteur de son niveau est de 10 cm.. Que deviendra le niveau de sable si vous le déplacez dans un récipient de même forme, mais avec une longueur de base 2 fois plus longue ?
Elle doit être raisonnée comme suit. La quantité de sable dans les premier et deuxième conteneurs n'a pas changé, c'est-à-dire que son volume y coïncide. Vous pouvez désigner la longueur de la base pour une... Dans ce cas, pour la première case, le volume de la substance sera :
V₁ = ha² = 10a²
Pour la deuxième boîte, la longueur de base est 2a, mais la hauteur du niveau de sable est inconnue :
V₂ = h (2a)² = 4ha²
Dans la mesure où V₁ = V₂, vous pouvez assimiler des expressions :
10a² = 4ha²
Après avoir annulé les deux membres de l'équation par a², on obtient :
En conséquence, le nouveau niveau de sable sera h = 10/4 = 2,5 cm.

Tâche 2.
ABCDA₁B₁C₁D₁ est le bon prisme. On sait que BD = AB₁ = 6√2. Trouvez la surface totale du corps.
Pour faciliter la compréhension des éléments connus, vous pouvez représenter une figure.
Puisque nous parlons du prisme correct, nous pouvons conclure qu'à la base il y a un carré avec une diagonale de 6√2. La diagonale de la face latérale a la même taille, par conséquent, la face latérale a également la forme d'un carré, égal à la base. Il s'avère que les trois dimensions - longueur, largeur et hauteur - sont égales. On peut conclure que ABCDA₁B₁C₁D₁ est un cube.
La longueur de toute arête est déterminée par la diagonale connue :
a = d / √2 = 6√2 / √2 = 6
La surface totale est trouvée par la formule pour un cube :
Sful = 6a² = 6 6² = 216

Tâche 3.
La salle est en cours de rénovation. On sait que son sol se présente sous la forme d'un carré d'une superficie de 9 m². La hauteur de la pièce est de 2,5 m Quel est le coût le plus bas pour tapisser une pièce si 1 m² coûte 50 roubles?
Puisque le sol et le plafond sont des carrés, c'est-à-dire des quadrangles réguliers, et que ses parois sont perpendiculaires aux surfaces horizontales, nous pouvons conclure qu'il s'agit d'un prisme régulier. Il est nécessaire de déterminer l'aire de sa surface latérale.
La longueur de la pièce est a = 9 = 3 m.
La zone sera recouverte de papier peint Côté = 4 · 3 · 2,5 = 30 m².
Le coût le plus bas du papier peint pour cette pièce sera 50 30 = 1500 roubles.
Ainsi, pour résoudre des problèmes sur un prisme rectangulaire, il suffit de pouvoir calculer l'aire et le périmètre d'un carré et d'un rectangle, ainsi que ses propres formules pour trouver le volume et la surface.
Comment trouver l'aire d'un cube